这篇讲的还是很(比较)清楚的吧~
适用范围:
给定的图存在负权边,这时类似Dijkstra等算法便没有了用武之地,而Bellman-Ford算法的复杂度又过高,SPFA算法便派上用场了。
我们约定有向加权图G不存在负权回路,即最短路径一定存在。当然,我们可以在执行该算法前做一次拓扑排序,以判断是否存在负权回路,但这不是我们讨论的重点。
算法思想:
我们用数组d记录每个结点的最短路径估计值,用邻接表来存储图G。
我们采取的方法是动态逼近法:设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止.
(其实就是一次一次的更新求min值)
复杂度:
期望的时间复杂度O(KE), 其中K为所有顶点进队的平均次数,可以证明K一般小于等于2。
(自信易证!!?)
实现方法:
建立一个队列,初始时队列里只有起始点,再建立一个表格记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为0)。
然后执行松弛操作,用队列里有的点作为起始点去刷新到所有点的最短路,如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。
判断有无负环:
如果某个点进入队列的次数超过N次则存在负环(SPFA无法处理带负环的图)
下面是一个例子:
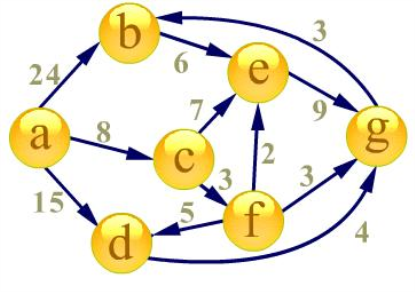
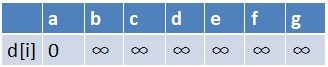
首先建立起始点a到其余各点的最短路径表格:
最开始源点a入队,当队列非空时:
1.队首元素(a)出队,
对以a为起始点的所有边的终点依次进行松弛操作(此处有b,c,d三个点)
此时路径表格状态为:
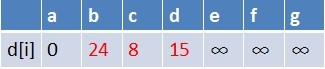
在松弛时三个点的最短路径估值变小了,而这些点队列中都没有出现,这些点需要入队,此时,队列中新入队了三个结点b,c,d:
2.队首元素b点出队,
对以b为起始点的所有边的终点依次进行松弛操作(此处只有e点)
此时路径表格状态为:
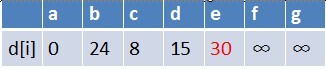
在最短路径表中,e的最短路径估值也变小了,e在队列中不存在,因此e也要
入队,此时队列中的元素为c,d,e;
3.队首元素c点出队,对以c为起始点的所有边的终点依次进行松弛操作(此处有e,f两个点)
此时路径表格状态为:
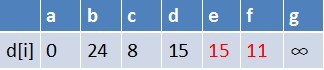
在最短路径表中,e,f的最短路径估值变小了,e在队列中存在,f不存在。
因此e不用入队了,f要入队,此时队列中的元素为d,e,f。
4.队首元素d点出队,对以d为起始点的所有边的终点依次进行松弛操作(此处只有g这个点)
此时路径表格状态为:
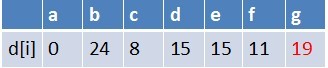
在最短路径表中,g的最短路径估值没有变小(松弛不成功,就是没有更新),没有新结点入队,队列中元素为f,g
5.队首元素f点出队,对以f为起始点的所有边的终点依次进行松弛操作(此处有d,e,g三个点)
此时路径表格状态为:
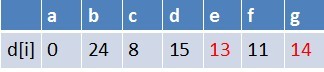
在最短路径表中,e,g的最短路径估值又变小,队列中无e点,e入队,队列中存在g这个点,g不用入队,此时队列中元素为g,e
6.队首元素g点出队,对以g为起始点的所有边的终点依次进行松弛操作(此处只有b点)
此时路径表格状态为:
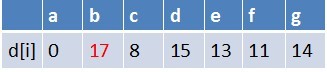
在最短路径表中,b的最短路径估值又变小,队列中无b点,b入队,
此时队列中元素为e,b
7.队首元素e点出队,对以e为起始点的所有边的终点依次进行松弛操作(此处只有g这个点)
此时路径表格状态为:
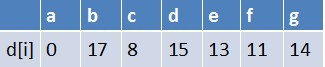
在最短路径表中,g的最短路径估值没变化(松弛不成功),此时队列中元素为b
8.队首元素b点出队,对以b为起始点的所有边的终点依次进行松弛操作(此处只有e这个点)
此时路径表格状态为:

在最短路径表中,e的最短路径估值没变化(松弛不成功),此时队列为空了。
最终a到g的最短路径为14。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69
| #include<cstdio> using namespace std; struct node {int x; int value; int next; }; node e[60000]; int visited[1505],dis[1505],st[1505],queue[1000]; int main() { int n,m,u,v,w,start,h,r,cur; freopen("c.in","r",stdin); freopen("c.out","w",stdout); while(scanf("%d%d",&n,&m)!=EOF) { for(int i=1;i<=1500;i++) {visited[i]=0; dis[i]=-1; st[i]=-1; } for(int i=1;i<=m;i++) { scanf("%d%d%d\n",&u,&v,&w); e[i].x=v; e[i].value=w; e[i].next=st[u]; st[u]=i; } start=1; visited[start]=1; dis[start]=0; h=0; r=1; queue[r]=start; while(h!=r) { h=(h+1)%1000; cur=queue[h]; int tmp=st[cur]; visited[cur]=0; while(tmp!=-1) { if (dis[e[tmp].x]<dis[cur]+e[tmp].value) { dis[e[tmp].x]=dis[cur]+e[tmp].value; if(visited[e[tmp].x]==0) { visited[e[tmp].x]=1; r=(r+1)%1000; queue[r]=e[tmp].x; } } tmp=e[tmp].next; } } printf("%d\n",dis[n]); } return 0; }
|
邻接表如上
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
| #include<iostream> #include<cstdio> using namespace std; int n,m,s,cnt,from,u,v,w,tail; int isin[100005],dis[100005],z[1000005],zn,h; int head[2000005]; struct E{ int w,next,to; }; E no[1000005]; void addedge(int u,int v,int w) { cnt++; no[cnt].to=v; no[cnt].next=head[u]; no[cnt].w=w; head[u]=cnt; } void spfa() { for(int i=1;i<=n;i++) dis[i]=2147483647; dis[from]=0; isin[from]=1; z[1]=from; zn++; while(h<zn) { int now=z[++h]; isin[now]=0; for(int i=head[now];i;i=no[i].next) { if(dis[now]+no[i].w<dis[no[i].to]) { dis[no[i].to]=dis[now]+no[i].w; if(isin[no[i].to]==0) { zn++; z[zn]=no[i].to; isin[no[i].to]=1; } } } } } int main() { scanf("%d%d%d",&n,&m,&from); for(int i=1;i<=m;i++) { scanf("%d%d%d",&u,&v,&w); addedge(u,v,w); } spfa(); for(int i=1;i<=n;i++) { printf("%d ",dis[i]); } return 0; }
|
链式前向星如上









