状态压缩
作为OIers,我们不同程度地知道各式各样的算法。
大部分问题的算法都有一个多项式级别的时间复杂度上界(如O(log n)),我们一般称这类问题为P类(deterministic Polynomial-time)问题,例如在有向图中求最短路径。
然而存在几类问题,至今仍未被很好地解决,人们怀疑他们根本没有多项式时间复杂度的算法,对这些问题尚不知有多项式时间的算法存在。
对于某些至今尚未找到多项式时间复杂度的算法,然而它们的应用又是如此的广泛,我们不得不努力寻找好的解决方案。毫无疑问,对于这些问题,使用暴力的搜索是可以得到正确的答案的,但在信息学竞赛那有限的时间内,很难写出速度可以忍受的暴力搜索。例如对于TSP问题,暴力搜索的复杂度是O(n!),如此高的复杂度使得它对于高于10的数据规模就无能为力了。那么,有没有一种算法,它可以在很短的时间内实现,而其最坏情况下的表现比搜索好呢?答案是肯定的——
状态压缩(States Compression,SC)。
1.首先安利一下基本运算符~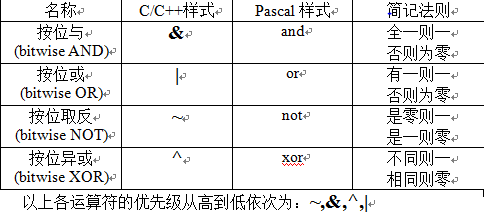
(特别关照了P选手2333)
2.上面东西的特殊应用
a) and:
i. 用以取出一个数的某些二进制位
ii. 取出一个数的最后一个1(lowbit) :x&-x
b) or :用以将一个数的某些位设为1
c) not:用以间接构造一些数:~0=4294967295=232-1
d) xor:
i. 不使用中间变量交换两个数:a=a^b;b=a^b;a=a^b;
ii. 将一个数的某些位取反
有了这些基础,就可以开始了。–(^-^)V
我们暂时避开状态压缩的定义,先来看一个小小的例题。
【引例】
在n*n(n≤20)的方格棋盘上放置n个车(可以攻击所在行、列),求使它们不能互相攻击的方案总数。
【分析】
这个题目之所以是作为引例而不是例题,是因为它实在是个非常简单的组合学问题:我们一行一行放置,则第一行有n种选择,第二行n-1,……,最后一行只有1种选择,根据乘法原理,答案就是n!。这里既然以它作为状态压缩的引例,当然不会是为了介绍组合数学。我们下面来看另外一种解法:状态压缩递推(States Compressing Recursion,SCR)。
我们仍然一行一行放置。取棋子的放置情况作为状态,某一列如果已经放置棋子则为1,否则为0。这样,一个状态就可以用一个最多20位的二进制数 表示。例如n=5,第1、3、4列已经放置,则这个状态可以表示为01101(从右到左)。设f[s]为达到状态s的方案数,则可以尝试建立f的递推关系。
考虑n=5,s=01101。这个状态是怎么得到的呢?因为我们是一行一行放置的,所以当达到s时已经放到了第三行。又因为一行能且仅能放置一个车,所以我们知道状态s一定来自:
①前两行在第3、4列放置了棋子(不考虑顺序,下同),第三行在第1列放置;②前两行在第1、4列放置了棋子,第三行在第3列放置;
③前两行在第1、3列放置了棋子,第三行在第4列放置。
这三种情况互不相交,且只可能有这三种情况。根据加法原理,f[s]应该等于这三种情况的和。写成递推式就是:
f[01101]=f[01100]+f[01001]+f[00101]
根据上面的讨论思路推广之,得到引例的解决办法:
f[0]=1
f[s]=∑f[s^2i]
其中s∈[0…01,1…11],s的右起第i+1位为1。
反思这个算法,其正确性毋庸置疑(可以和n!对比验证)。但是算法的时间复杂度为O(n2n),空间复杂度O(2n),是个指数级的算法,比循环计算n!差了好多,它有什么优势?较大的推广空间。
Sample Problems
【例1】
在n*n(n≤20)的方格棋盘上放置n个车,某些格子不能放,求使它们不能互相攻击的方案总数。
【分析】
对于这个题目,确实存在数学方法(容斥原理),但因为和引例同样的理由,这里不再赘述。
联系引例的思路,发现我们并不需要对算法进行太大的改变。引例的算法是在枚举当前行(即s中1的个数,设为r)的放置位置(即枚举每个1),而对于例1,第r行可能存在无法放置的格子,怎么解决这个问题呢?枚举1的时候判断一下嘛!事实的确是这样,枚举1的时候判断一下是否是不允许放置的格子即可。
但是对于n=20,O(n2n)的复杂度已经不允许我们再进行多余的判断。所以实现这个算法时应该应用一些技巧。对于第r行,我们用a[r]表示不允许放置的情况,如果某一位不允许放置则为1,否则为0,这可以在读入数据阶段完成。运算时,对于状态s,用tmps=s^a[r]来代替s进行枚举,即不枚举s中的1转而枚举tmps中的1。因为tmps保证了无法放置的位为0,这样就可以不用多余的判断来实现算法,代码中只增加了计算a数组和r的部分,而时间复杂度没有太大变化。
这样,我们直接套用引例的算法就使得看上去更难的例1得到了解决。你可能会说,这题用容斥原理更快。没错,的确是这样。但是,容斥原理在这题上只有当棋盘为正方形、放入的棋子个数为n、且棋盘上禁止放置的格子较少时才有简单的形式和较快的速度。如果再对例1进行推广,要在m\*n的棋盘上放置k个车,那么容斥原理是无能为力的,而SCR算法只要进行很少的改变就可以解决问题 。这也体现出了引例中给出的算法具有很大的扩展潜力。
【例2】
给出一个n*m的棋盘(n、m≤80,n*m≤80),要在棋盘上放k(k≤20)个棋子,使得任意两个棋子不相邻。每次试验随机分配一种方案,求第一次出现合法方案时试验的期望次数,答案用既约分数表示。
【分析】
显然,本题中的期望次数应该为出现合法方案的概率的倒数,则问题转化为求出现合法方案的概率。而概率= ,方案总数显然为C(n*m,k),则问题转化为求合法方案数。整理一下,现在的问题是:在n*m的棋盘上放k个棋子,求使得任意两个棋子不相邻的放置方案数。
这个题目的状态压缩模型是比较隐蔽的。观察题目给出的规模,n、m≤80,这个规模要想用SC是困难的,若同样用上例的状态表示方法(放则为1,不放为0),280无论在时间还是在空间上都无法承受。然而我们还看到n\*m≤80,这种给出数据规模的方法是不多见的,有什么玄机呢?能把状态数控制在可以承受的范围吗?稍微一思考,我们可以发现:9\*9=81>80,即如果n,m都大于等于9,将不再满足n\*m≤80这一条件。所以,我们有n或m小于等于8,而28是可以承受的。我们假设m≤n(否则交换,由对称性知结果不变)n是行数m是列数,则每行的状态可以用m位的二进制数表示。但是本题和例1又有不同:例1每行每列都只能放置一个棋子,而本题却只限制每行每列的棋子不相邻。但是,上例中枚举当前行的放置方案的做法依然可行。我们用数组s[1..num] 保存一行中所有的num个放置方案,则s数组可以在预处理过程中用DFS求出,同时用c[i]保存第i个状态中1的个数以避免重复计算。开始设计状态。如注释一所说,维数需要增加,原因在于并不是每一行只放一个棋子,也不是每一行都要求有棋子,原先的表示方法已经无法完整表达一个状态。我们用f[i][j][k]表示第i行的状态为s[j]且前i行已经放置了k个棋子 的方案数。沿用枚举当前行方案的做法,只要当前行的方案和上一行的方案不冲突即可,“微观”地讲,即s[snum[i]]和s[snum[i-1]]没有同为1的位,其中snum[x]表示第x行的状态的编号。然而,虽然我们枚举了第i行的放置方案,但却不知道其上一行(i-1)的方案。为了解决这个问题,我们不得不连第i-1的状态一起枚举,则可以写出递推式:
f[0][1][0]=1;
f[i][j][k]=∑f[i-1][p][k-c[j]]
其中s[1]=0,即在当前行不放置棋子;j和p是需要枚举的两个状态编号,且要求s[j]与s[p]不冲突,即s[j]&s[p]=0。
当然,实现上仍有少许优化空间,例如第i行只和第i-1行有关,可以用滚动数组节省空间。
有了合法方案数,剩下的问题就不是很困难了,需要注意的就只有C(n*m,k)可能超出64位整数范围的问题,这可以通过边计算边用GCD约分来解决,具体可以参考附件中的代码。这个算法时间复杂度O(n*pn*num2),空间复杂度(滚动数组)O(pn*num),对于题目给定的规模是可以很快出解的。
然后是一道状压DP…
P1052 过河
1.这里讲一种蒟蒻好懂的离散化的方法。
看到这题的第一想法肯定是简单的线性DP,用f[i]表示到第i位最少能经过几个石子,data[i]表示第i位是否有石子,所有f[i]初始化无限大,f[0]初始化0
那么显然f[i]=min(f[i],f[j]+data[i]),其中j枚举i-s到i-t的位置,而且确保j大于等于0
这样结果就是在f[(l-t)~l]中取最小值
这道题有一个很大的特点,就是要跳的距离L非常大(10^9)而每次跳的距离非常小(10)
{这青蛙似乎很累}
所以假如直接这样搞的话连内存都承受不了,时间复杂度同样直接炸破天际。
但是我们发现,这道题最多只有100个石子,这也就是说在这巨大的L中石子的分布非常稀疏
而跳的距离又非常的小,那么显然这青蛙要跳很多步才会遇到一个需要考虑的石子。
这时候我们证明2个命题来完成题目
1:把L的值改为最后一个石子的位置加1,不影响问题的解
{这是显然的,因为只要跳到最后一个石子之后就可以随便跳}
2:当s不等于t时,如果我们要从x开始,考虑下一个的石子位置在y,那么把x到y直接大于t的部分都裁掉,不影响问题的解
{把y-x表示成kt+b的形式,假如b不为0那这个石子显然没有考虑的价值,因为显然有避开的策略,把距离改为t仍然可以避开,所以只有b等于0时才对问题的解有影响。此时由于s是不等于t的,那么我们只要控制每次跳不全为t就可以解决问题 ,也就是说k与问题是无关的,因为我们只关心在在什么时候跳出一段不为t的距离}
通过上面的方法,我们就可以保证任意让个石子的距离不超过t
这样L的规模在s不等于t时就被压缩到了10*100+1的范围
(所以其实这道题的数据规模算是非常小的)
所以我们就能在限定的时间和内存之内用DP解决当s不等于t时问题了
当s等于t的时候,也就是说这个青蛙跳的轨迹是固定的,那么只要O(n)判断一个石子是否在青蛙跳过的轨迹上就可以了
2.状压
此题初看是一个典型的搜索题。从河的一侧到河的另一侧,要找最少踩到的石头数。但从数据范围来看。1..10^9长度的桥。就算是O(n)的算法也不能在一秒内出解。
如果搜索石子,方法更困难。这要考虑到前面以及后面连续的石子。若换一种方法。用动态规划,以石子分阶段的一维动规,时间复杂度是O(n^2)。最多也只有100×100的时间。但是这样分状态就十分复杂。因为石头的分布是没有任何规律,而且会有后效性。
这样只好有回到搜索。搜索石子会和动规一样没有规律。我们一桥的长度为对象进行搜索,然后再加上一个巧妙的剪枝就可以在很短的时间内出解。可以号称为O(m^2)。
[题目实现]
先以时间为对象进行搜索。时间复杂度为O(L)。从桥的一侧到另一侧,中间最多只有100个石子。假设桥长为最大值(10^9),石头数也为最大值(100)。这样中间一定会有很多“空长条” (两个石子中的空地),处理时把这些跳过,就只会有M次运算。关键是找出每一个可以跳过的“空长条”。
我们可以先把青蛙可以跳出的所有可能求出,然后就可以求出可以忽略的“空长条”。
F[i]=Min{F[i-s]………f[i-t]} (如果i为石子,那么加1,否则不加1)这样f[l]即为所求,注意初始值f[0..s-1]为一个较大的数,f[s…t-1]为他们本身的值。(有石头为1,没有石头为0)
但由于n较大直接动规会超时。所以要将n压缩
查看坐标,可以发现,如果b[i]-b[i-1]>t,显然对于b[i-1]+t<n<b[i],a[n]总是等于a[b[i-1]]..a[b[i-1]+t]中的数,因此可对其进行压缩。
|
|